How to multiply tensors wihout doing so? (1/3)

Let’s use these two simple 2nd-order tensors.

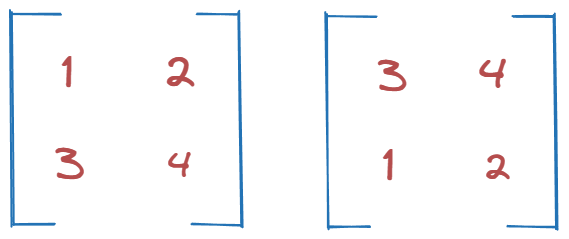
After multiplying them we get:

import torch
t1 = torch.tensor([[1, 2], [3, 4]])
t2 = torch.tensor([[3, 4], [1, 2]])
t1@t2

tensor([[ 5,  8],
        [13, 20]])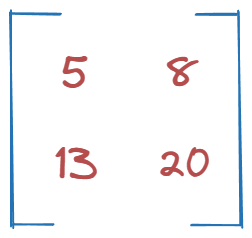

Simple.

But we’ve used a magic symbol @! That’s a big no-no.

What’s happening there?

How about we don’t do that?

As you probably know, naively looping over tensors, multiplying elements one by one, summing them, and then putting them into a new tensor of the correct size is a bad idea.

Instead, we will start by transposing the second tensor (rotating it over its ‘identity’ axis).

t2 = t2.T
t2

tensor([[3, 1],
        [4, 2]])

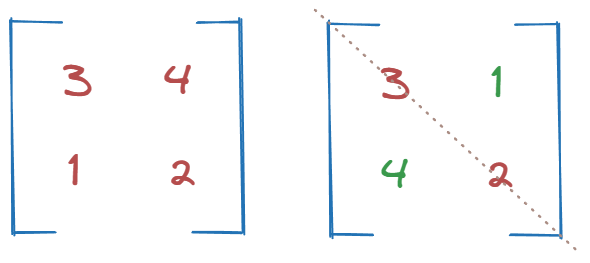
Why? We’ll see in a bit.

Now we want to add a dummy dimension to both tensors. We want the first tensor’s shape to be [2, 1, 2], and the second to be [1, 2, 2].

We can simply reshape them or achieve that by adding two pairs of brackets to the first one and one pair of brackets to the second.

t1 = t1.reshape((2, 1, 2)) # torch.tensor([[[1, 2]], [[3, 4]]])
t2 = t2.reshape((1, 2, 2)) # torch.tensor([[[3, 4], [1, 2]]])

t1, t2, t1.shape, t2.shape

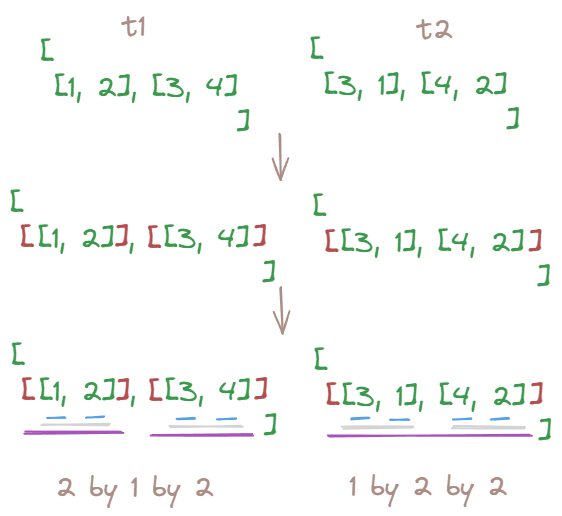
tensor([[[1, 2]],

        [[3, 4]]])
tensor([[[3, 1],
         [4, 2]]])
torch.Size([2, 1, 2]) torch.Size([1, 2, 2])

Let’s multiply them now (element-wise).

t3 = t1 * t2

What will come out of it exactly?

Multiplication rules tell us that multiplying a [2, 1, 2] tensor by a [1, 2, 2] one is indeed possible and will result in a [2, 2, 2] tensor.

Broadcasting rules

Each tensor has at least one dimension.
When iterating over the dimension sizes, starting at the trailing dimension, the dimension sizes must either be equal, one of them is 1, or one of them does not exist.

As we can see, this operation doesn’t brake any rules. The second dimension in the first tensor and the first dimension in the second tensor will be expanded. Importantly, this does not make any copies of the data.

As a side note, it’s good to remember that in-place operations do not allow the in-place tensor to change shape.

Multiplication rules in this type of scenario can be a bit tricky at first, but here it is quite streightforward.

High-level overview:
Multiply A by CD block and B by CD block. Then just put them side by side. This again uses broadcasting.

You can simplify it furher:

Multiply A * C. Then you multiply A * D and append it to the frist vector.

Now do the same with B. B * C, B * D, append.

Since B ‘is in’ a different dimension than A, the resulting tensor will be seperate from the previous one. They will be appended together as two 2-by-2 blocks.

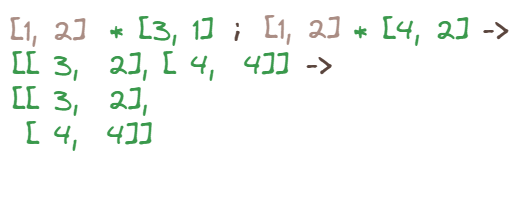
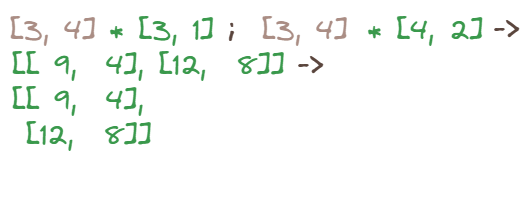
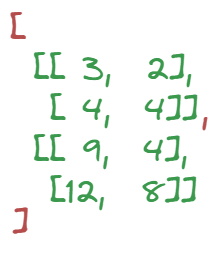
Both (1.) and (2.) will, sort of, take care of increasing the size of the second dimension of the second tensor to 2:
[2, 1, 2] -> [2, 2, 2]
(3.) will do the same thing but to the first dimension of the first tensor:
[1, 2, 2] -> [2, 2, 2]

We need to do one last thing, which is to sum that tensor over its last dimension (third one).

t3.sum(dim=2)

This will shrink all the vectors in the last dimension to scalars by summing all the numbers inside.

Since the keepdim flag in sum() is set to False by default, dimensions of size 1 will be squizzed out, leaving us with a tensor of size [2, 2].

t3.sum(dim=2).shape

torch.Size([2, 2])

If we set it to True, the resulting tensor’s shape would be [2, 2, 1].

t3.sum(dim=2, keepdim=True).shape

torch.Size([2, 2, 1])

Let’s stick with the defaults here.

Final result, after the summation and squeezing out the last dimension:

t3.sum(dim=2)

tensor([[ 5,  8],
        [13, 20]])

It’s exactly the same as with @!

But why?

Does it work for all shapes and is it really what happens under the hood?

Find out in the second part of this blog!