On why it works:
Well, we can’t use @ — that’s not a thing.
What is something in math that looks like it can be handy? Probably *.
As you know, when multiplying matrices, the rows are ‘dot producted’ with the columns. That’s not the behavior of *.
In order to fix that, we can try transposing the second tensor.
Let’s see what we can do after this operation, just by multiplying together vectors inside each tensor.

Standard matmul for reference:
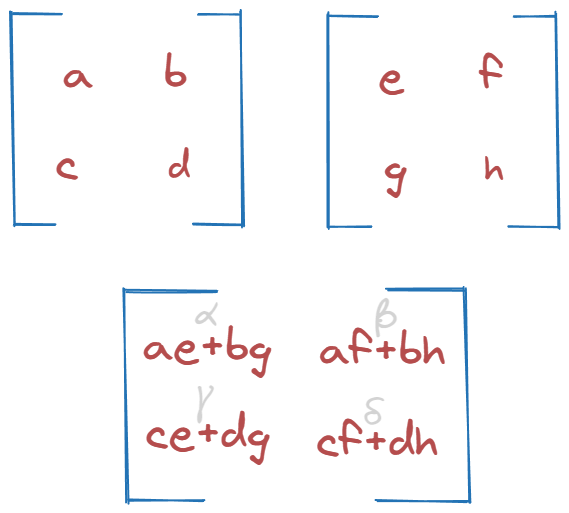
Our tensors (right one already transposed):
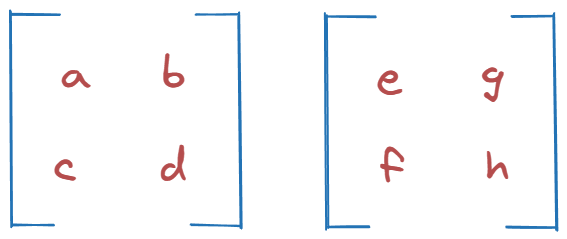
Let’s try to * them.
Result:
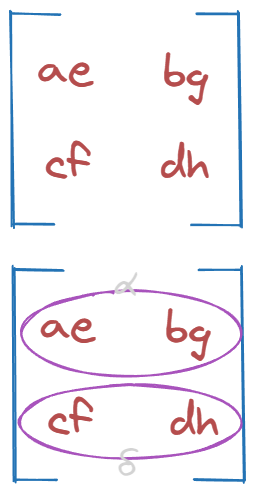
First pair looks like α. Second one like δ. We’re onto something.
But this is only the first part of the puzzle.
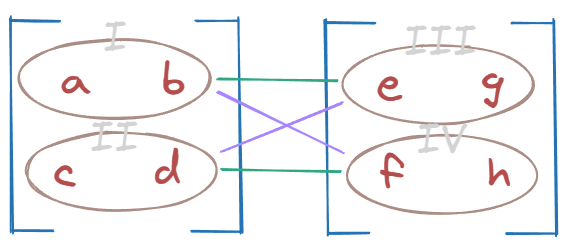
We multiplied I by III and II by IV.
It seems we also need to multiply I by IV and II by III.
How can we impose this behavior?
We can split the first tensor into two parts to ensure that when we multiply all the pieces both I and II will be multiplied with the entire second tensor (utilizes broadcasting). This is why previously, in the second step, we changed the dimensions of the first tensor to [2, 1, 2].
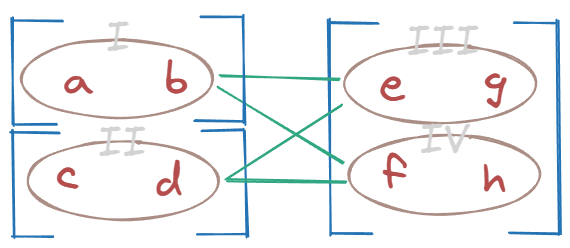
Changing the shape of the second tensor to [1, 2, 2], just like we did before, is technically not needed. The additional dimension at the front will be added implicitly.
Result:
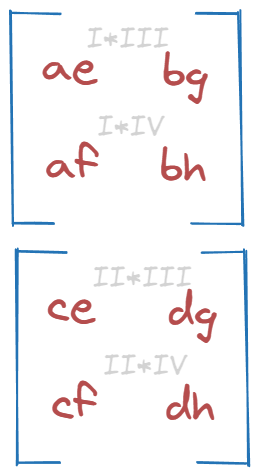
Comparison with matmul reference:
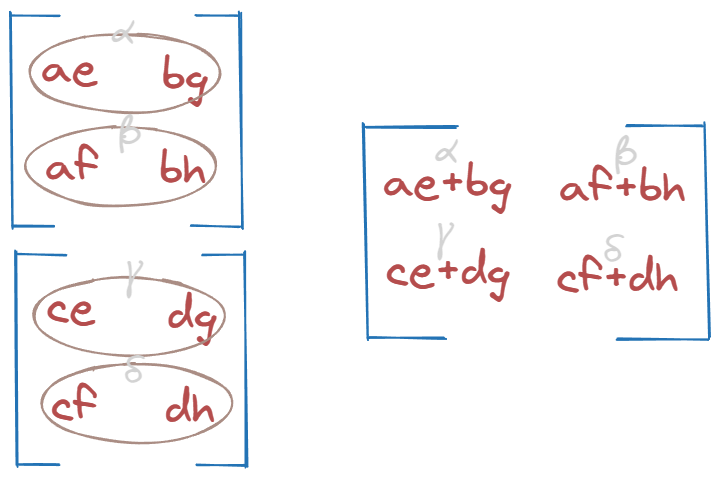
We’re almost there.
α and β should go together. Same goes for γ and δ.
Naturally, we want to sum them up. Let’s do it over the last dimension (third one).
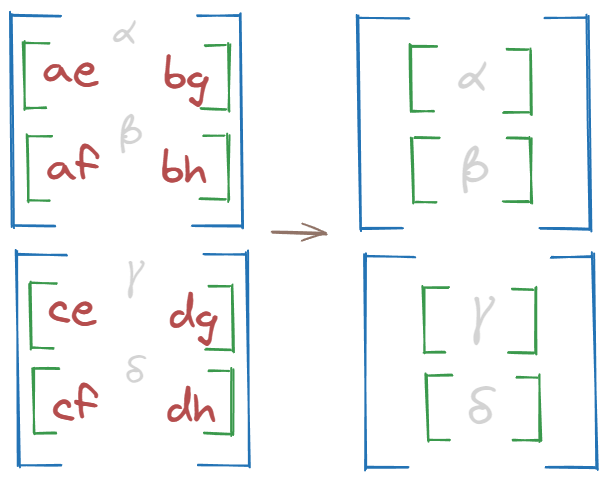
Close! They’re not yet together. We need to squeeze out the dimension of size 1 we just created.
This will combine the correct parts:
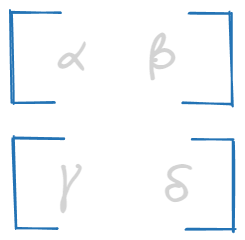
Final result compared to matmul reference:
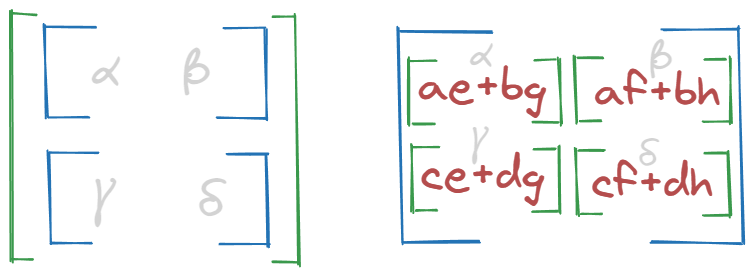
Voilà.
But are libraries using something like this under the hood?
Part 3 it is.